Problem Statement
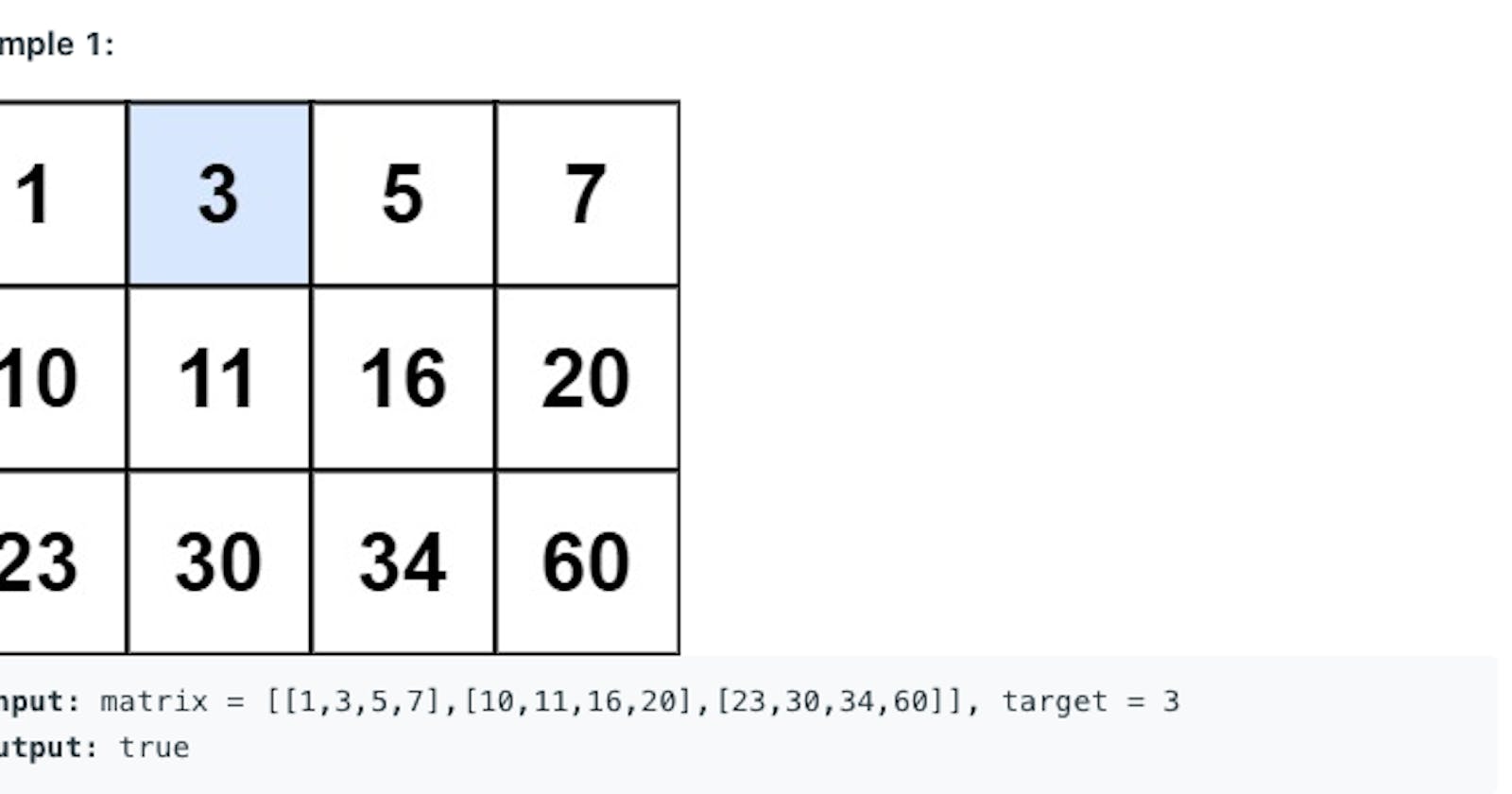
Write an efficient algorithm that searches for a value in an m x n matrix. This matrix has the following properties:
- Integers in each row are sorted from left to right.
- The first integer of each row is greater than the last integer of the previous row.
Approach
Brute Force
This is the first thing that comes to mind.
Traverse the matrix's each row and column value by value and get the number.
Time Complexity: O$(n^2)$
Now the question is, can I optimise this?
Why do I need to optimise, because the problem clearly says, write an efficient algorithm.
So, let's try to write an efficient algorithm.
Optimised Approach
What I can figure out is there's no way of traversing the array other than an outer for loop, that will traverse each row.
But what I can think of is using the first property of the matrix.
Integers in each row are sorted from left to right.
Since the array is sorted, I can use Binary Search to search for the value, and the complexity of this search binary search is O(logn)
As of now the complexity of this solution stands at $O(n) + O(logn) = O(nlogn)$
Now again the same question, can I optimise it even further?
If I am thinking correctly, I can leverage the second point of the problem statement as well i.e.,
The first integer of each row is greater than the last integer of the previous row.

So, the idea is same, if the searched number is smaller than the current element than it's definitely in the previous collection.
So, I have to do binary search on columns as well, and complexity again becomes
$O(logn)$
So, adding row search with column search, we get
O$(logn)$ + O$(logn)$ = O$(logn)$
Implementation
/**
* @param {number[][]} matrix
* @param {number} target
* @return {boolean}
*/
const binarySearchOnColumn = (matrix , target) => {
if(matrix.length === 1) {
return matrix;
}
const columnSize = matrix.length;
let midOfColumn = Math.floor(columnSize/2);
let slicedArray;
if(matrix[midOfColumn][0] > target ) {
slicedArray = matrix.slice(0 , midOfColumn);
} else {
slicedArray = matrix.slice(midOfColumn, matrix.length)
}
const finalMatrix = binarySearchOnColumn(slicedArray, target);
return finalMatrix;
}
const binarySearchOnRow = (workingArray,target)=>{
if (workingArray.length === 1) {
return workingArray[0] === target;
}
const rowSize = workingArray.length;
let midOfRow = Math.floor(rowSize / 2);
let sliceArray;
if (workingArray[midOfRow] > target) {
slicedArray = workingArray.slice(0, midOfRow);
} else {
slicedArray = workingArray.slice(midOfRow, workingArray.length)
}
return binarySearchOnRow(slicedArray, target);
}
var searchMatrix = function(matrix, target) {
const workingRow = binarySearchOnColumn(matrix , target);
const isElementFound = binarySearchOnRow(workingRow[0], target);
return isElementFound;
};
Results
Next Steps
If you find my thought process helpful, do tell me in the comments and don't forget to follow me on Twitter @sagars_01